The Cars Dataset

Here we’ll use the classic Cars dataset to illustrate different ways Gumbi can be used.

import gumbi as gmb
import seaborn as sns
import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
plt.style.use(gmb.style.breve)

from warnings import filterwarnings

# Suppress a weird warning from seaborn
filterwarnings("ignore", message="No data for colormapping provided via 'c'. Parameters 'norm' will be ignored")

WARNING (pytensor.tensor.blas): Using NumPy C-API based implementation for BLAS functions.

Read in some data and store it as a Gumbi DataSet:

cars = sns.load_dataset('mpg').dropna().astype({'weight':float, 'model_year':float})

ds = gmb.DataSet(cars,
                 outputs=['mpg', 'acceleration'],
                 log_vars=['mpg', 'acceleration', 'weight', 'horsepower', 'displacement'])

Create a Gumbi GP object:

gp = gmb.GP(ds)

Now we’re ready to fit, predict, and plot against various dimensions in our datset.

Simple regression

gp.fit(outputs=['mpg'], continuous_dims=['horsepower']);

X = gp.prepare_grid()
y = gp.predict_grid();

pp = gmb.ParrayPlotter(X, y)
pp.plot()
sns.scatterplot(data=cars, x='horsepower', y='mpg', color=sns.cubehelix_palette()[-1], alpha=0.5);

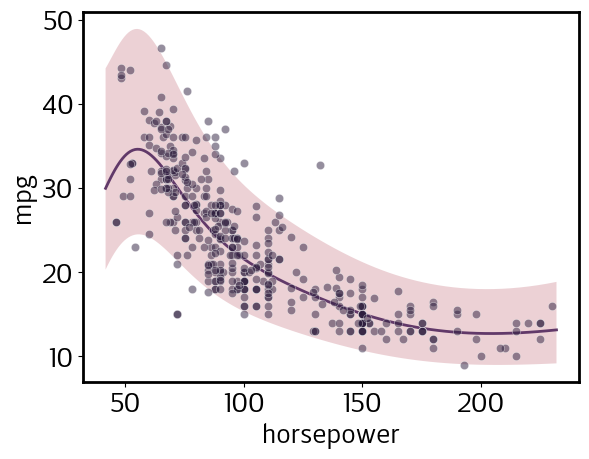
Note that, despite the error bands appearing wider at lower values of horsepower, this actually is a homoskedastic model; i.e., predicted noise does not depend on the input value. However, because we declared mpg among the log_vars when we defined our DataSet, the model is homoskedastic in log space. Let’s plot log(mpg) to illustrate this:

pp.y_scale = 'transformed'
pp.y_tick_scale = 'transformed'
pp.update()
pp.plot()

sns.scatterplot(data=cars.assign(mpg=np.log(cars.mpg)), x='horsepower', y='mpg', color=sns.cubehelix_palette()[-1], alpha=0.5);

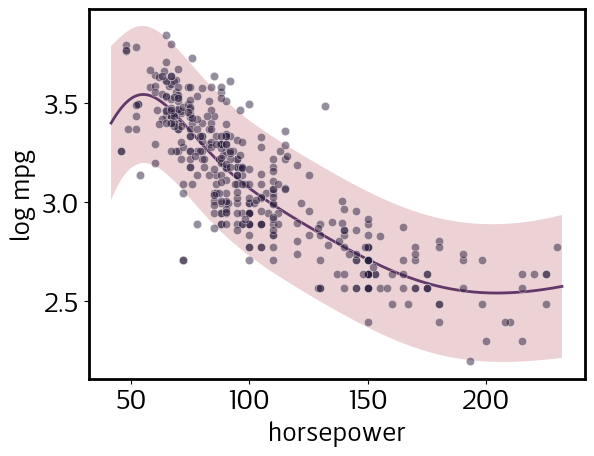
We declared horsepower to be a log_var as well. Let’s view both mpg and horsepower in log-space, but retain the natural-space tick labels for easier interpretation.

pp.y_tick_scale = 'natural'
pp.x_scale = 'transformed'
pp.update()
pp.plot()

sns.scatterplot(data=cars.assign(mpg=np.log(cars.mpg), horsepower=np.log(cars.horsepower)), x='horsepower', y='mpg', color=sns.cubehelix_palette()[-1], alpha=0.5);

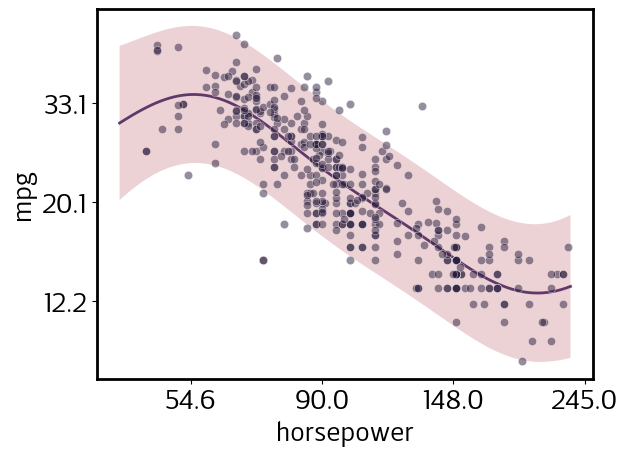
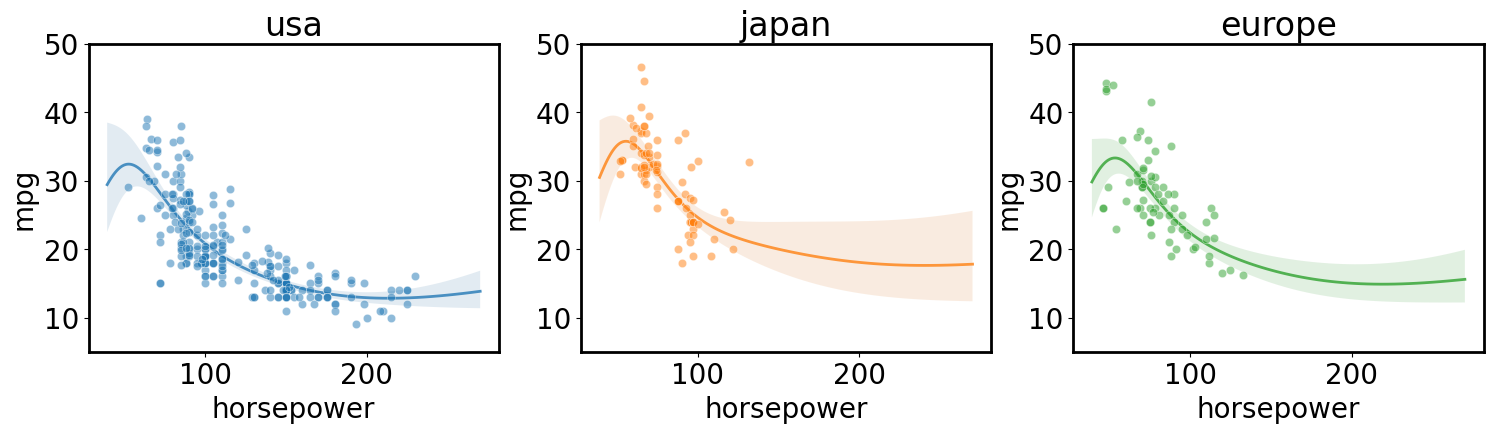
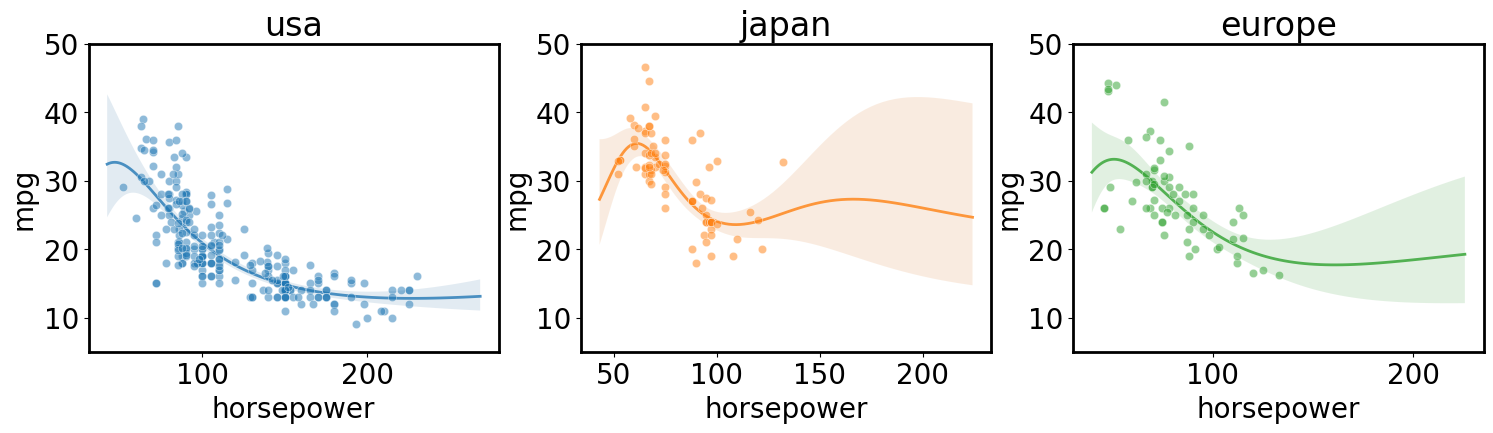
Independent regression for each class in a category

axs = plt.subplots(1,3, figsize=(18, 4))[1]
for i, (ax, origin) in enumerate(zip(axs, cars.origin.unique())):
    gp.fit(outputs=['mpg'], categorical_dims=['origin'], categorical_levels={'origin': origin}, continuous_dims=['horsepower']);
    X = gp.prepare_grid()
    y = gp.predict_grid(with_noise=False)

    gmb.ParrayPlotter(X, y).plot(ax=ax, palette=sns.light_palette(f'C{i}'))

    sns.scatterplot(data=cars[cars.origin==origin], x='horsepower', y='mpg', color=f'C{i}', alpha=0.5, ax=ax);
    ax.set_title(origin)
    ax.set_ylim([5, 50])

Correlated multi-input regression across different classes in a category

gp.fit(outputs=['mpg'], categorical_dims=['origin'], continuous_dims=['horsepower']);

X = gp.prepare_grid()
axs = plt.subplots(1,3, figsize=(18, 4))[1]
for i, (ax, origin) in enumerate(zip(axs, cars.origin.unique())):
    y = gp.predict_grid(categorical_levels={'origin': origin}, with_noise=False)

    gmb.ParrayPlotter(X, y).plot(ax=ax, palette=sns.light_palette(f'C{i}'))

    sns.scatterplot(data=cars[cars.origin==origin], x='horsepower', y='mpg', color=f'C{i}', alpha=0.5, ax=ax);
    ax.set_title(origin)
    ax.set_ylim([5, 50])

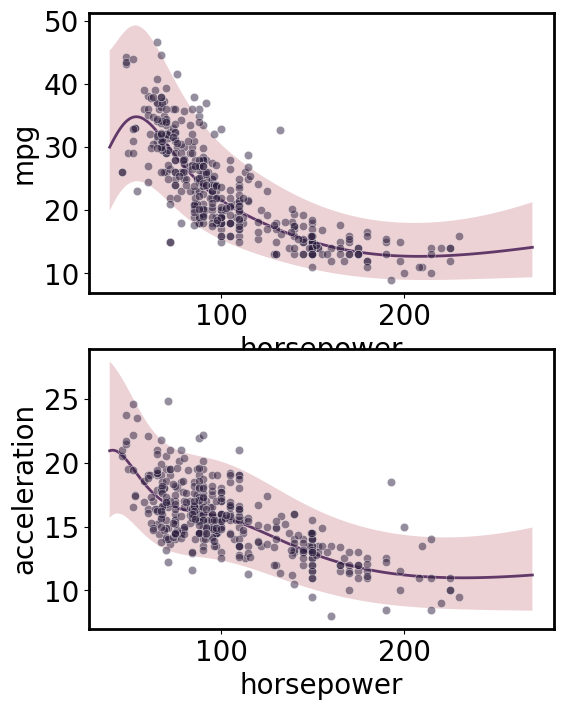
Multi-output regression

gp.fit(outputs=['mpg', 'acceleration'], continuous_dims=['horsepower']);

X = gp.prepare_grid()
Y = gp.predict_grid()

axs = plt.subplots(2,1, figsize=(6, 8))[1]
for ax, output in zip(axs, gp.outputs):
    y = Y.get(output)

    gmb.ParrayPlotter(X, y).plot(ax=ax)

    sns.scatterplot(data=cars, x='horsepower', y=output, color=sns.cubehelix_palette()[-1], alpha=0.5, ax=ax);

Correlated multivariate sampling from joint predictions

X = gp.parray(horsepower=[50, 100, 150, 200])
gp.predict_points(X)
y = gp.predictions

samples_df = pd.concat(
    [pd.DataFrame(point.dist.rvs(10000, random_state=j).as_dict()).assign(horsepower=hp.values()) for j, (point, hp) in enumerate(zip(y, X))],
    ignore_index=True)

sns.pairplot(samples_df, hue='horsepower', kind='kde', corner=True, plot_kws={'levels': 1});

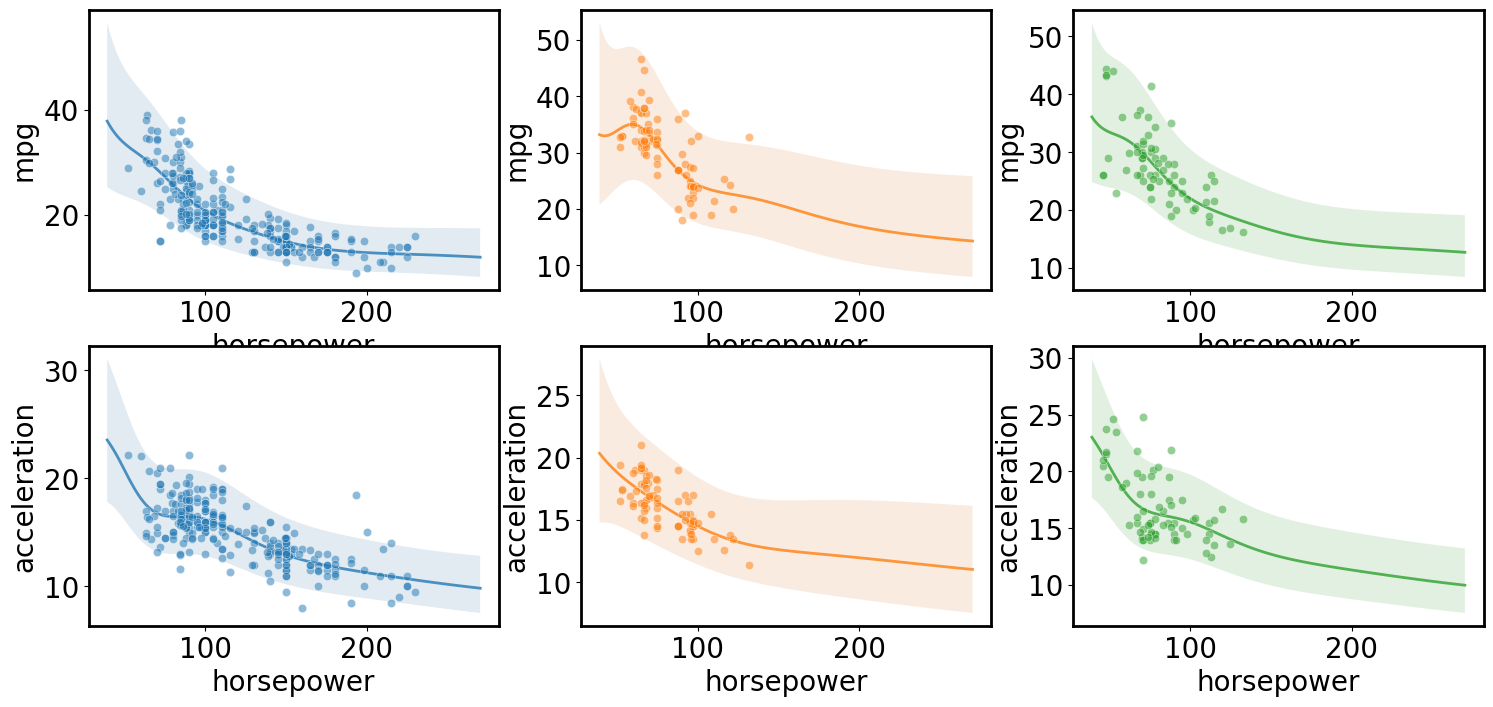
Multi-input multi-output regression

gp.fit(outputs=['mpg', 'acceleration'], categorical_dims=['origin'], continuous_dims=['horsepower'], linear_dims=['horsepower']);

X = gp.prepare_grid()
axs = plt.subplots(2,3, figsize=(18, 8))[1]
for i, (row, origin) in enumerate(zip(axs.T, cars.origin.unique())):
    Y = gp.predict_grid(categorical_levels={'origin': origin})
    for ax, output in zip(row, gp.outputs):
        y = Y.get(output)

        gmb.ParrayPlotter(X, y).plot(ax=ax, palette=sns.light_palette(f'C{i}'))

        sns.scatterplot(data=cars[cars.origin==origin], x='horsepower', y=output, color=f'C{i}', alpha=0.5, ax=ax);

Multi-dimensional regression

from matplotlib.colors import Normalize
norm = Normalize()
norm(ds.wide.mpg);

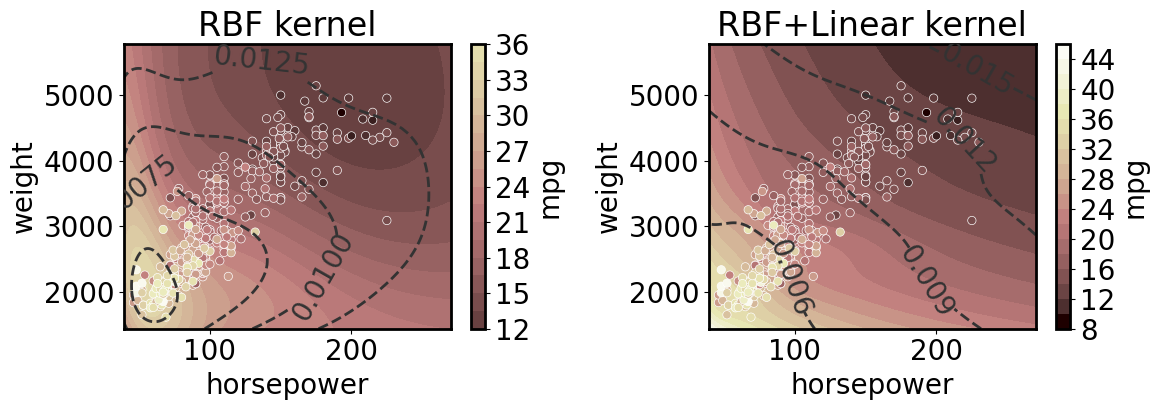
2D regression with and without linear kernel

Note that here we plot the coefficient of variation (with respect to aleatoric and epistemic uncertainty together) as dashed lines.

axs = plt.subplots(1,2, figsize=(12, 4.5))[1]
for ax, linear in zip(axs, [False, True]):
    linear_dims = ['horsepower','weight'] if linear else None

    gp.fit(outputs=['mpg'], continuous_dims=['horsepower','weight'], linear_dims=linear_dims);

    XY = gp.prepare_grid()
    X = XY['horsepower']
    Y = XY['weight']
    z = gp.predict_grid()

    plt.sca(ax)
    pp = gmb.ParrayPlotter(X, Y, z)
    pp(plt.contourf, levels=20, cmap='pink', norm=norm)
    pp.colorbar(ax=ax)

    cs = ax.contour(X.values(), Y.values(), z.σ/z.μ, levels=4, colors='0.2', linestyles='--')
    ax.clabel(cs)

    sns.scatterplot(data=cars, x='horsepower', y='weight', hue='mpg', palette='pink', norm=norm, ax=ax);
    ax.legend().remove()

    title = 'RBF+Linear kernel' if linear else 'RBF kernel'
    ax.set_title(title)

plt.tight_layout()

3D regression with 2D predictions

Note that here we plot the epistemic uncertainty as dashed lines.

cylinders = cars.cylinders.unique()
cylinders.sort()

axs = plt.subplots(1, 5, figsize=(30, 4.5))[1]

gp.fit(outputs=['mpg'], continuous_dims=['horsepower','weight', 'cylinders'], linear_dims=['horsepower','weight', 'cylinders']);

for ax, cyl in zip(axs, cylinders):

    XY = gp.prepare_grid(at=gp.parray(cylinders=cyl))
    X = XY['horsepower']
    Y = XY['weight']
    z = gp.predict_grid(with_noise=False)

    plt.sca(ax)
    pp = gmb.ParrayPlotter(X, Y, z)
    pp(plt.contourf, levels=20, cmap='pink', norm=norm)
    pp.colorbar(ax=ax)

    cs = ax.contour(X.values(), Y.values(), z.σ, levels=4, colors='0.2', linestyles='--')
    ax.clabel(cs)

    sns.scatterplot(data=cars[cars.cylinders==cyl], x='horsepower', y='weight', hue='mpg', palette='pink', norm=norm, ax=ax);
    ax.legend().remove()

    title = 'RBF+Linear kernel' if linear else 'RBF kernel'
    ax.set_title(f'{cyl} Cylinders')

plt.tight_layout()